需对以上四个出题逐个判别，根据有两条，一是向量数量积的界说；二是向量加法与减法的平行四边形法则。

  ∴θ=0或π，∴ ∥ 且以上各步均可逆，故出题（1）是线）若 ， 反向，则 、 的夹角为π，∴ · =｜ ｜·｜ ｜cosπ=－｜ ｜·｜ ｜且以上各步可逆，故出题（2）是线）当 ⊥ 时，将向量 ， 的起点确定在同一点，以向量 ， 为邻边作平行四边形，则该平行四边形必为矩形，所以它的两条对角线的长持平，即有｜ + ｜＝｜ － ｜。反过来，若｜ + ｜＝｜ － ｜，则以 ， 为邻边的四边形为矩形，所以有 ⊥ ，因而出题（3）是线）当｜ ｜＝｜ ｜，但 与 的夹角和 与 的夹角不等时，就有｜ · ｜≠｜ · ｜，故出题（4）是假出题。

  两向量同向时，夹角为0（或0°），而反向时，夹角为π（或180°）；两向量笔直时，夹角为90°，因而当两向量共线或π，反过来若两向量的夹角为0或π，则两向量共线。

  使用平面向量的数量积的界说，性质及运算律可直接求 · ，（ － ） 2 ，求 + ，应先求 + 2 ，再开方。

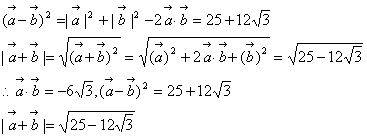
  ）2 =a2 ±2a·b+b2这一公式的使用，别的还需留意求模的办法。例4.已知向量 +3 笔直于向量7 －5 ，向量 －4 笔直于向量7 －2 ，求向量 与 的夹角。

  要求 与 的夹角，首先要求出 与 的夹角的余弦值，即要求出｜ ｜、｜ ｜及 · ，而本题中很难求出｜ ｜、｜ ｜及 · ，但由公式cosθ= 可知，若能把 · ，｜ ｜及｜ ｜中的两个用另一个表示出来，即可求出余弦值，然后可求得 与 的夹角θ。

  设 与 的夹角为θ。∵ +3 笔直于向量7 －5 ， －4 笔直于7 －2 ，

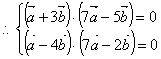
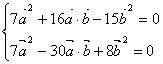
  xO y 中，若定点A（1，2）与动点P（x，y）满意 ，则点P的轨道方程是_________________。（2）已知直线 与圆O: 相交于A、B两点，且 ，则 ___________。剖析：第（2）小题关键是运用几许法求出两向量的夹角，再运用向量的数量积公式即可。

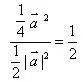
  7.已知 = （ ，－1）， =（ ），且存在实数k和t，使得x= ＋（t 2 －3） ，y=－k ＋t ，且x⊥y，试求 的最小值。

  本题具有综合性，要留意仔细观察标题傍边的条件，使用笔直这一突破口，列出方程求解k与t的关系式。留意：本题中a

  b虽然有坐标，但假如直接求出x与y的坐标再用x·y=0求解，则进程太杂乱，应先求解a

  相同点：向量的数量积与实数的乘积均满意交换律和分配律；两个向量与两个实数都合适以下关系式：

  ；；不同点：（1）从“形”和“数”两方面看，数量积的几许含义是一个向量的长度乘以另一个向量在该向量地点直线上的投影；从坐标方式看，如设

  都是实数，而与不一定共线。而实数运算满意结合律。（3）并不能导出或，可导出如下四种或许：

  且可得到，只要就契合题意，并不一定有。而实数运算中且。求最值常用的24种办法，主张一切高中生都要保藏！！